An indicator of the increasing popularity of kanban is the number of software tools and online services that claim kanban functionality. For those practitioners who have seen the tremendous benefits of kanban, this should be a gratifying development. But what does it really mean for a tool to support or to enable kanban? And what about those features that are claimed to be “kanban” features but, in reality, have little to do with or are antithetical to kanban? I present in this article some criteria for assessing whether a tool really supports the kanban method or if it is just using kanban for window dressing.
Here is a summary of the key areas of difference between a tool that supports kanban and a tool that does not:
- Visualization of value streams
- Facilitating pulling of work
- Probabilistic management
- Queue management
This is not meant to be an exhaustive feature list or a checklist for assessing kanban tools. Rather, these are the key areas that help us distinguish between true support of kanban and a cargo cult-like use of tools.
How is a tool intended to be used?
When a software tool is designed, its functionality is based on certain use cases that the designers believe correspond to the needs of the targeted users. The tool is built with the intention to be used in a certain way, according to those use cases.
Some tools are built with the intention to support the kanban method for managing the flow of work. Other tools are built with the intention to support a non-kanban way of managing the flow of work.
The intended use of the tool is reflected in the data structures it manages, the business logic of its processing, the user interface—indeed, all the levels of the tool’s architecture. However, as the tool evolves, additions are made to those various levels. As we will see below, it is possible to change the user interface, for example, without changing the underlying business logic or data structures. The effort to please more users and sell more licenses can lead to a sort of cognitive dissonance in the use of the tool. The user interface might be telling you that you are using the kanban method, while the business logic or the tool’s utility is based on a push method for managing flow.
There might be a use for such hybridization in tools. I do not mean to imply that there are right tools and wrong tools. Tools can help or hinder their users, depending on their intended use and the manner in which the user employs them.
For the organizations that seek a new tool to support a kanban initiative, remember that one swallow does not a summer make. Consider all levels of the architecture of a tool when deciding which one to use. Consider how the designers intended the tool to be used and compare this to your intended use. With that in mind, let us look at some of the major areas that distinguish tools supporting the kanban method from tools supporting other methods of managing flow.
Visualization of value streams
We know that visualization of the state of work is a key principle of kanban. Often, visualization is the only kanban feature in use in an organization. But many tools use the word “kanban” to describe their visualization features when they are not supporting kanban at all. This leads to an unfortunate adulteration of the term “kanban.”
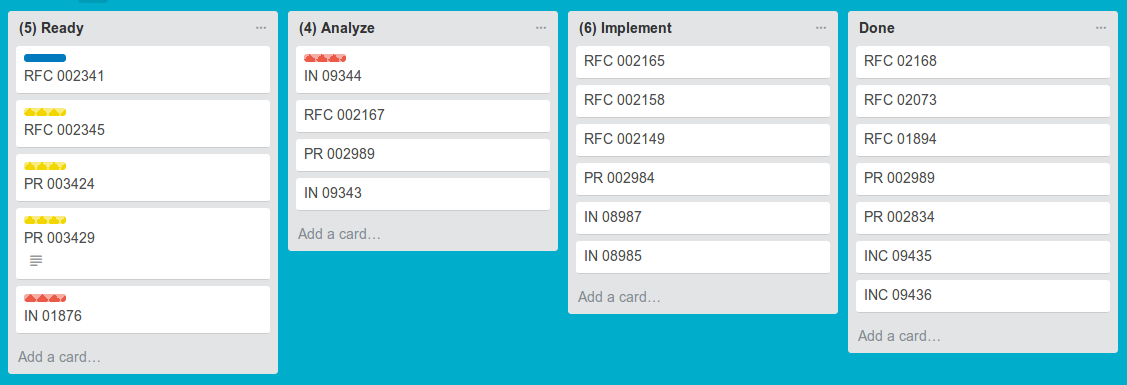
The classical visualization of the flow of work is a matrix where each phase of a value stream corresponds to a column. The column headers contain various types of control and policy information, such as phase names, WIP limits, and entry and exit criteria. In addition, there may be more than one row or swim lane, corresponding to different types of work or to variants of the value stream. Finally, each work item is represented by a card that is moved from column to column in accordance with its status in the value stream.
For many practitioners, this visualization of the status of work is called a “kanban board.” Others prefer to call it a “card board” (see Fig. 1).
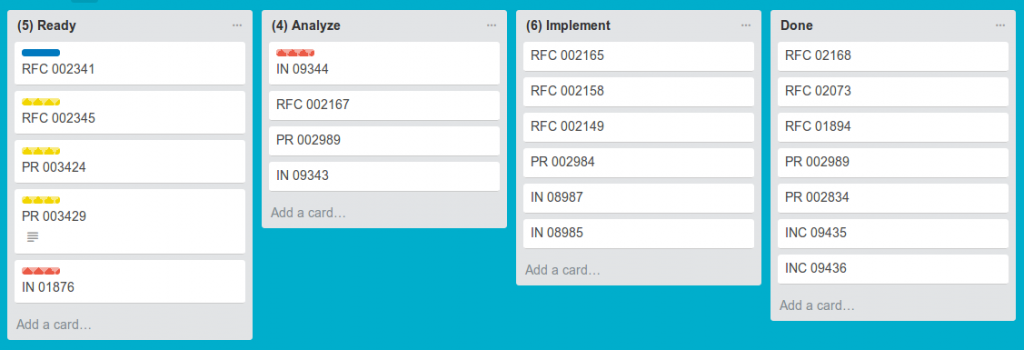
The issue is that many tools offer a visualization of work in a matrix format that uses columns and rows in ways that are very different from what I have just described. And yet, the editors of these tools call them kanban boards. For example, a tool might display work items in a calendar format. Each column is really just a date or range of dates (see Fig. 2). Viewers cannot see WIP limits, either by value stream phase or by the workers. Cards are placed by some principle other than value stream phase, such as by task deadline. Such ways of organizing work are antithetical to kanban, according to which most tasks are not likely to have deadlines at all.
If a tool is advertised as having a “kanban-style” display board, investigate further what that really means.
Pulling work
Pulling work, rather than pushing work, is a central concept of kanban. Without the principle of pulling work, many features of kanban become difficult, or even impossible, to implement. Examples of these features include a just-in-time organization of work flow, the use of WIP limits and giving teams the authority to commit to work (or not).
Animation of pulling work in a tool supporting kanban
In spite of this, some tools proclaim their support of kanban, even though their business logic is fundamentally based on the concept of pushing work. What, then, is the difference in the tools between pulling and pushing?
Animation of pushing work in a tool not supporting kanban
When a tool is designed to support pushing work, it asks upstream users to define the characteristics and requirements of downstream tasks. These upstream users include such roles as process owners, process managers, incident owners, service level managers, or simply the practitioners in the previous, upstream task. The workers responsible for those downstream tasks are not given the responsibility to decide when and how to do that work. Instead, they are presented with a set of obligations. These obligations generally include such things as the priority to assign the work, the maximum acceptable duration for the work, who shall do the work, and deadlines for completing the work. Thus, each worker or team of workers has little autonomy in deciding how and when to do the work. They have only to comply with regulations and constraints defined by others.
Of course, it is always possible to correct errors made upstream. But the need to change the constraints and controls on work leads to ping-ponging work and the waste of performing non-value adding activities, handing-off work, doing rework, waiting and getting authorizations from other stakeholders. Although advanced non-kanban tools may have features designed to reduce these levels of waste, they serve to reduce agility and increase the effort required to set up and maintain the tools. This is a classic issue with saving-the-paradigm-type activities. Kanban obviates the need for such features in supporting tools.
Deterministic versus probabilistic management
There is another issue closely related to pulling work versus pushing work. This is the question of whether work should be managed in a deterministic way or in a probabilistic way.
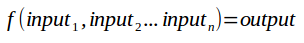
Fig. 3: Determinism is like a mathematical function, with unambiguously defined inputs and a single output
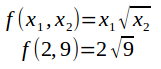
Determinism is like a mathematical function where a set of inputs yields a single output (see Figs. 3 and 4). Deterministic management makes the assumption that there is a best way for an organization to perform tasks and to organize those tasks into processes. An organization might align itself with so-called “best practice” frameworks, or it might formulate its own “best” way of working. A deterministic manager might say, “If only we all follow exactly our defined processes in a reliable and consistent way, then everything will turn out alright.”
Tools supporting deterministic management typically have three features designed to limit the variability in processes:
- They attempt to constrain the inputs to services, forcing them into known and pre-determined categories
- They measure and report on the actual execution of work in comparison with the idealized, “best” practice
- They provide automations designed to enforce compliance with “best” practice
In short, tools supporting deterministic management:
- Record a set of rules for how work shall be done
- Attempt to enforce conformity with those rules
- Measure the level of conformity with those rules
For example, suppose a deterministically managed organization decides that a certain task, when performed “correctly”, shall not take more than four hours to complete. The supporting tool will record four hours as the acceptable level of service and measure the durations of each instance of that task. It might issue warnings when work is on the brink of exceeding the defined duration. It might inform management when there are breaches of agreed levels of service.
Some tools are more proactive. They break down the task into small components. In addition, they provide a control structure for:
- Informing the workers what to do
- Recording when those activities have been completed.
- Possibly automating the execution of some of those activities
In typical deterministic management tools, the control structure takes the form of a process whose tasks are focused inwardly, on the technical aspects of doing work. This contrasts with tools whose value stream focuses on the customer and adding value to the output of work.
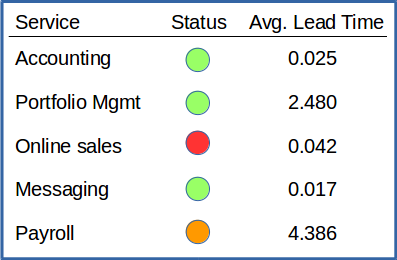
Deterministic management tools are characterized by dashboards with green/amber/red lights to show instantaneous work status (for example, see Fig. 5). When viewed from the perspective of the Cynefin framework, such dashboards present an image of work as if it were all obvious or, at worst, complicated. The reality of what is complex or chaotic is hidden behind the false security of a simple colored circle.
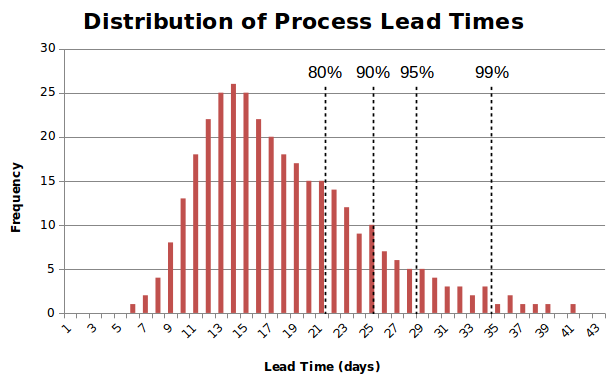
In probabilistic management, we can no longer assume that inputs and outputs have fixed values. They have, instead, probabilities of falling in a certain range. We want to understand the distribution of these values for a given sample (as in Fig. 6).
Unlike deterministic management, probabilistic management focuses on the overall throughput in completing work rather than on compliance of activities with rules. It assumes that variability in tasks is inevitable and follows a measurable distribution. There is variability in terms of:
- When tasks are ready to be performed,
- The specific parameters of the tasks
- The availability of workers to perform the tasks.
Probabilistic management is not so much concerned with whether a single instance of a task breaches a limit. Instead, it is concerned with the distribution of task lead times (see, for example, Fig. 6).
Of course, probabilistic management shares with deterministic management the goal of doing work more quickly and more accurately. However, it focuses on finding ways of completing more work and getting the output to customers more quickly.
Deterministic managers, in contrast, often focus on keeping workers busy. This form of management is based on the fallacious assumption that the busier they are the more quickly work will be finished. Queuing theory, as used in kanban, demonstrates that the reality is just the opposite.
Consequently, tools that support kanban will help make it easy to identify blockages in the flow of work (see below), rather than identifying individual breaches in service levels. They do not try to measure and manage worker performance on a phase by phase basis. Instead, they measure mean levels of overall performance, mean levels of work in progress and mean levels of throughput.
Queue management
In a management system based on kanban, the size of input queues is a critical parameter for understanding how long it will take to perform work. A kanban tool will typically make the size of each queue highly visible. Queue size is immediately visible on a card board, in addition to the synoptic views used by managers. It is true that non-kanban tools typically display queues and might provide real-time reporting on queue size (see Fig. 7). However, such reporting is common only for service desk queues.


Tools supporting kanban differ by virtue of their features used to manage those queues. This management takes several forms:
- Defining WIP limits
- Managing flow autonomously
- Defining queues relative to value stream phases
- Applying queue management theory, such as Little’s Law
- Managing blockages with greater maturity
- Agilely managing work item priority
Autonomous management of WIP limits
In the use case of a team following the kanban method, changing the WIP limits is under the control of the team. Incremental changes to WIP limits from time to time are simple, low in risk and perfectly normal. The tool makes it easy for the team to do this tuning. The team does not require authorization from some controlling process or management role to make such modifications.
In the use case where a tool is not supporting kanban, it probably does not even provide for defining WIP limits. Furthermore, any changes to the parameters that are supposed to influence work throughput, such as operational level agreements, are complicated affairs involving negotiations between upstream and downstream teams and controls by service level managers. In this use case, changes are likely to be subject to the control of a change management process. As a result, the team has little autonomy in managing these parameters. This complexity makes for much more rigid management systems, whereas kanban supports much greater levels of agility.
How queues are defined
Another major difference concerns how the queues are defined. In a kanban tool, queues are related to the phases of the value stream. In a non-kanban tool, queues are related to the organizational units performing work, irrespective of the value stream of the work.
A caveat should be mentioned, however. In many cases, an organization is structured in alignment with its value streams. For example, a value stream might include the phases Analyze, Build, Test, Deploy. Each of those phases might have a specialized team responsible for that work. In such cases of specialization, value stream phase queues would be identical to organizational queues. But that sort of specialization, which is less common in small organizations, is increasingly being questioned. There is an increasing tendency for teams to become less specialized, where a single team might be responsible for an entire value stream. As we approach this latter form of organizational structure, the distinction in how the queue is defined becomes much more significant.
Queuing theory and Little's Law
When a tool supports the kanban approach it potentially uses such queue management principles as Little’s Law1 to make predictions about when a work item is likely to be completed, and with what probability. Non-kanban tools do not make such calculations, relying instead on prescriptive or deterministic information about when a work item should be completed. This type of information often encourages the management behavior of pressuring workers to work harder or work longer hours, the issue known in a lean context as muri.
Managing blockages
A non-kanban tool typically has only the most primitive of features for managing queues and their blockages. It simply provides means for visualizing a queue and easily selecting the next work item in the queue, typically based on pre-defined priorities. The only real queue management feature is the ability to sort and the queue according to various criteria. But nothing is done to help manage the size or contents of the queue.2
In a typical non-kanban use case, there are commonly two responses to work that is blocked or progressing too slowly:
- Pressure workers to work harder and longer
- Increase resources
These “techniques” are stressful, expensive and not very scalable.
Kanban provides a framework for a more sophisticated approach to unblocking work, largely derived from Eliyahu Goldratt’s Theory of Constraints:
- Identify the capacity constrained resource
- Protect the capacity constrained resource
- Subordinate upstream replenishment
- Buffer upstream activities
- Increase resources
These steps are typically supported by kanban tools in several ways:
- The card board readily shows where work is blocked. It suffices to identify a pattern where blocked work is often being performed by the same person, who would be the capacity constrained resource. In addition, kanban tools could collect data about resource liquidity, albeit tools do not commonly implement this functionality.
- Protecting that resource is virtually automatic when using kanban. By definition, the capacity constrained resource will simply not pull more work so long as his or her WIP limit is already reached.
- Subordinating upstream replenishment is, once again, very simple with kanban. It suffices to adjust the upstream WIP limits.
- Buffering of activities, too, is very simple with kanban. Buffers are simply additional columns on the card board.
Non-kanban tools do little or nothing to protect resources, subordinate replenishment or buffer activities. This is largely because these techniques are antithetical to flow management based on pushing work. The response of a manager if he or she saw work in a buffer would likely be, “Why isn’t anyone working on that task!?”
Managing work item priority
Non-kanban tools generally support the selection of the next work item to perform in two ways. Firstly, each item is provided with a priority and possibly with a due date. Often, the priority is made visible in the tool by special colors, fonts or another formatting. Secondly, queues can be sorted and filtered so as to easily see which is the next work item to select.
The difficulty with this approach is that it does not encourage an understanding of the contents of the work item and its value for the customer. Since the prioritization scheme is generally very simple (for example, priorities 1, 2, 3 and 4), it relies on a FIFO approach to select among items with the same priority. In the end, these tools provide a simple means for making fast or even automated decisions, with little understanding of the underlying issues. They are more concerned with the question of when to start doing work than with the question of how quickly work can be finished.
A kanban tool typically supports a more agile approach to selecting the next work item, generally based on the class of service of the work item. There might be a superficial resemblance between a priority and a class of service, especially for the case of a priority 1 task in a push system, as compared to a pre-emptive or expedited class of service in a pull system. But there the resemblance ends. A priority is essentially a numerical proxy metric for ordering a queue and deciding when to start work on an item. A class of service is essentially a means of helping to assess the risk of not finishing a work item when it is needed, or for optimizing the overall throughput of work by a team. Thus, the kanban aphorism, “stop starting and start finishing.”
Conclusion
The analysis I have made here is based on the assumption that tools are used according to their editors’ intention. It is possible, for example, to use a screwdriver as a chisel, but that is inefficient and ineffective, if not dangerous, over the long term. Similarly, it is possible to abuse both kanban and non-kanban tools, failing to benefit from their features or using them ineffectively. I set aside these abusive uses. They are, at best, exceptions that prove the rules.
Tools are created with specific use cases in mind. If those use cases are aligned with the kanban method, then it makes sense to describe the tool as a kanban tool. But if the use cases are antithetical to kanban, then a mere veneer of kanban-like features will not make the tool a kanban tool.
The goal of this article is not to provide a checklist to answer the question, “Is this a kanban tool or not?” Such a question is of very little use. Tools have little intrinsic value. Their value lies almost entirely in how they are used. If you use a tool to push work and to manage deterministically, you are not using that tool to support the kanban method, no matter what functionality that tool might have.
Just as Monsieur Jourdain was delighted to learn that he was using prose every day, so I hope the reader will delight in the use of the kanban method, supported by tools that genuinely help to use that method.
![]() The article When is a kanban tool not a kanban tool? by Robert S. Falkowitz, including all its contents, is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.
The article When is a kanban tool not a kanban tool? by Robert S. Falkowitz, including all its contents, is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.
Notes:
1 The kanban variant of Little’s Law is “The mean delivery rate (of work items) equals the Work in Progress (WIP) divided by the mean lead time.”
2 In typical non-kanban tools, where the queues are defined relative to organizational units, there may be automatic means of assigning a work item to a queue. This automation is generally done via models or templates, although we are starting to see the use of machine learning to automate queue assignment. Such ML techniques are largely superfluous in a kanban tool, where the card board makes it perfectly clear which queue comes next.